Robust Generalization with Adaptive Optimal Transport Priors for Decision-Focused Learning

Few-shot learning requires models to generalize under limited supervision while remaining robust to distribution shifts. Existing Sinkhorn Distributionally Robust Optimization (DRO) methods provide theoretical guarantees but rely on a fixed reference distribution, which limits their adaptability. We propose a Prototype-Guided Distributionally Robust Optimization (PG-DRO) framework that learns class-adaptive priors from abundant base data via hierarchical optimal transport and embeds them into the Sinkhorn DRO formulation. This design enables few-shot information to be organically integrated into producing class-specific robust decisions that are both theoretically grounded and efficient, and further aligns the uncertainty set with transferable structural knowledge. Experiments show that PG-DRO achieves stronger robust generalization in few-shot scenarios, outperforming both standard learners and DRO baselines.

Efficient Causal Structure Learning via Modular Subgraph Integration

Learning causal structures from observational data remains a fundamental yet computationally intensive task, particularly in high-dimensional settings where existing methods face challenges such as the super-exponential growth of the search space and increasing computational demands. To address this, we introduce VISTA (Voting-based Integration of Subgraph Topologies for Acyclicity), a modular framework that decomposes the global causal structure learning problem into local subgraphs based on Markov Blankets. The global integration is achieved through a weighted voting mechanism that penalizes low-support edges via exponential decay, filters unreliable ones with an adaptive threshold, and ensures acyclicity using a Feedback Arc Set (FAS) algorithm. The framework is model-agnostic, imposing no assumptions on the inductive biases of base learners, is compatible with arbitrary data settings without requiring specific structural forms, and fully supports parallelization. We also theoretically establish finite-sample error bounds for VISTA, and prove its asymptotic consistency under mild conditions. Extensive experiments on both synthetic and real datasets consistently demonstrate the effectiveness of VISTA, yielding notable improvements in both accuracy and efficiency over a wide range of base learners.

Alternating Differentiation for Optimization Layers

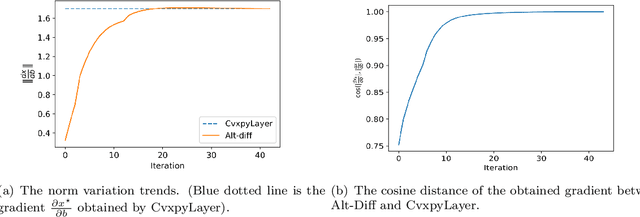
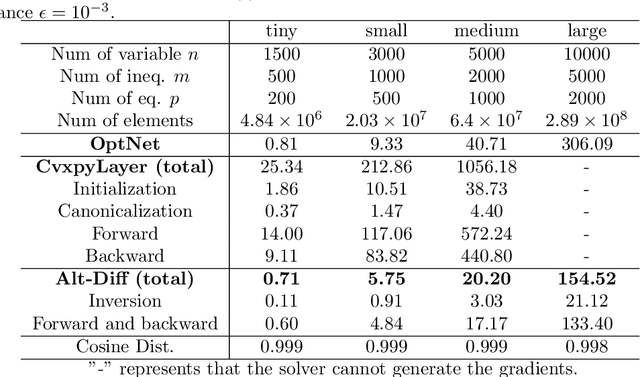
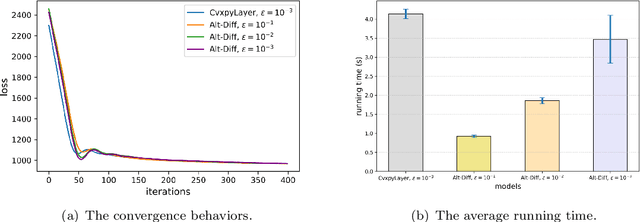
The idea of embedding optimization problems into deep neural networks as optimization layers to encode constraints and inductive priors has taken hold in recent years. Most existing methods focus on implicitly differentiating Karush-Kuhn-Tucker (KKT) conditions in a way that requires expensive computations on the Jacobian matrix, which can be slow and memory-intensive. In this paper, we developed a new framework, named Alternating Differentiation (Alt-Diff), that differentiates optimization problems (here, specifically in the form of convex optimization problems with polyhedral constraints) in a fast and recursive way. Alt-Diff decouples the differentiation procedure into a primal update and a dual update in an alternating way. Accordingly, Alt-Diff substantially decreases the dimensions of the Jacobian matrix and thus significantly increases the computational speed of implicit differentiation. Further, we present the computational complexity of the forward and backward pass of Alt-Diff and show that Alt-Diff enjoys quadratic computational complexity in the backward pass. Another notable difference between Alt-Diff and state-of-the-arts is that Alt-Diff can be truncated for the optimization layer. We theoretically show that: 1) Alt-Diff can converge to consistent gradients obtained by differentiating KKT conditions; 2) the error between the gradient obtained by the truncated Alt-Diff and by differentiating KKT conditions is upper bounded by the same order of variables' truncation error. Therefore, Alt-Diff can be truncated to further increases computational speed without sacrificing much accuracy. A series of comprehensive experiments demonstrate that Alt-Diff yields results comparable to the state-of-the-arts in far less time.